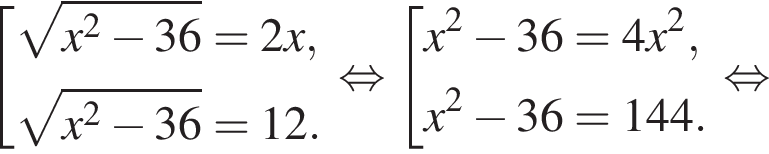
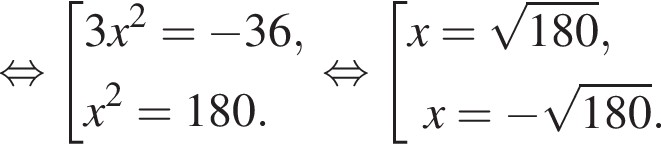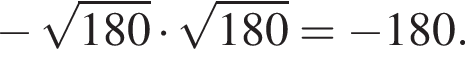Определите наименьшее натуральное число, кратное 2, которое при делении на 15 с остатком дает неполное частное, равное 3.
На клетчатой бумаге с клетками размером 1 см х 1 см изображён параллелограмм. Найдите его площадь в квадратных сантиметрах.
Среди точек
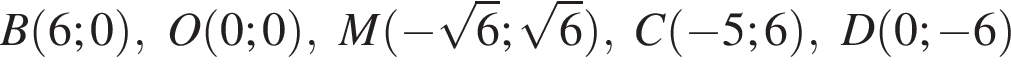 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Найдите значение выражения 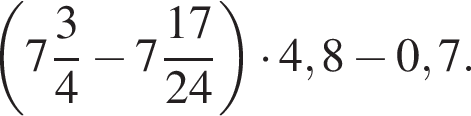
Если 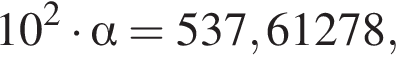 то значение α с точностью до сотых равно:
то значение α с точностью до сотых равно:
На рисунке изображены развернутый угол AOM и лучи OB и OC. Известно, что ∠AOC = 94°, ∠BOM = 126°. Найдите величину угла BOC.
Образующая конуса равна 16 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.

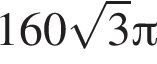
От листа жести, имеющего форму квадрата, отрезали прямоугольную полосу шириной 7 дм, после чего площадь оставшейся части листа оказалась равной 30 дм2. Длина стороны квадратного листа (в дециметрах) была равна:
Одна из сторон прямоугольника на 7 см длиннее другой, а его площадь равна 78 см2. Уравнение, одним из корней которого является длина меньшей стороны прямоугольника, имеет вид:
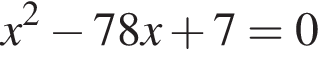 ;
;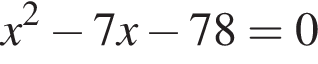 ;
;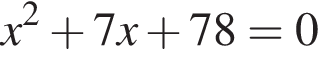 ;
;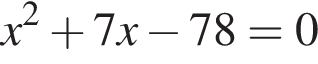 ;
;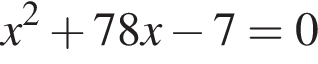 .
.Точки A(-3;3) и B(4;1) — вершины квадрата ABCD. Периметр квадрата равен:
Четырехугольник MNPK, в котором ∠N=136°, вписан в окружность. Найдите градусную меру угла K.
Решением неравенства
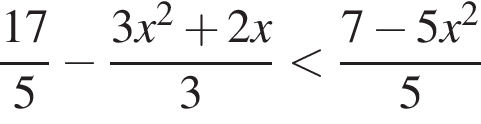
является промежуток:

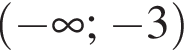
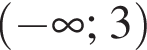
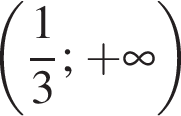
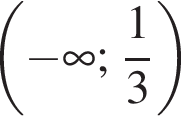
Параллельно стороне треугольника, равной 5, проведена прямая. Длина отрезка этой прямой, заключенного между сторонами треугольника, равна 2. Найдите отношение площади полученной трапеции к площади исходного треугольника.
Упростите выражение 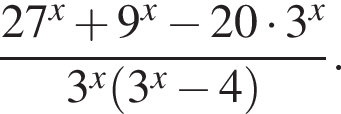
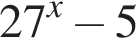
Найдите сумму целых решений неравенства 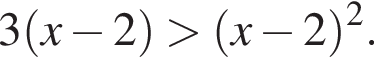
Какая из прямых пересекает график функции 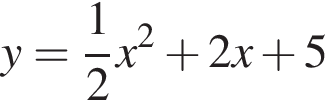 в двух точках?
в двух точках?

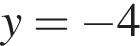

Сумма наибольшего и наименьшего значений функции
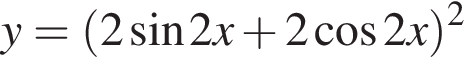
равна:
Найдите наименьший положительный корень уравнения 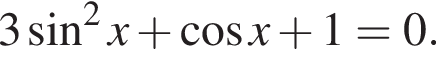
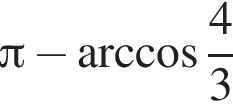
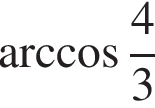
Автомобиль проехал некоторое расстояние, израсходовав 24 л топлива. Расход топлива при этом составил 9 л на 100 км пробега. Затем автомобиль существенно увеличил скорость, в результате чего расход топлива вырос до 12 л на 100 км. Сколько литров топлива понадобится автомобилю, чтобы проехать такое же расстояние?
Решите уравнение  В ответ запишите сумму его корней (корень, если он один).
В ответ запишите сумму его корней (корень, если он один).
Основание остроугольного равнобедренного треугольника равно 4, а синус противоположного основанию угла равен 0,6. Найдите площадь треугольника.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
По двум перпендикулярным прямым, которые пересекаются в точке O, движутся две точки M1 и M2 по направлению к точке O со скоростями 1 ![]() и 2
и 2 ![]() соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 2 м, M2O = 9 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 2 м, M2O = 9 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
Найдите количество корней уравнения 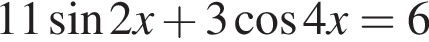 на промежутке
на промежутке 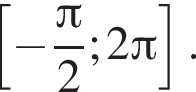
Четырёхугольник ABCD вписан в окружность. Если 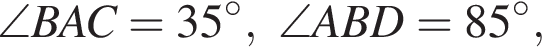 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Найдите сумму наименьшего и наибольшего целых решений неравенства 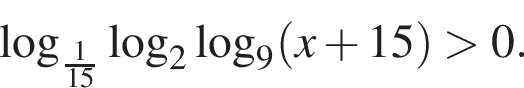
В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с четными номерами на 130 больше суммы членов с нечетными номерами. Найдите сотый член этой прогрессии.
Из точки А проведены к окружности радиусом ![]() касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 15S.
касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 15S.
Из двух растворов с различным процентным содержанием спирта массой 100 г и 900 г отлили по одинаковому количеству раствора. Каждый из отлитых растворов долили в остаток другого раствора, после чего процентное содержание спирта в обоих растворах стало одинаковым. Найдите, сколько раствора (в граммах) было отлито из каждого раствора.
Найдите произведение корней уравнения 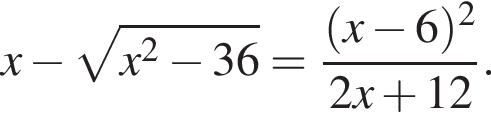

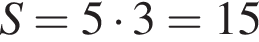 см2.
см2.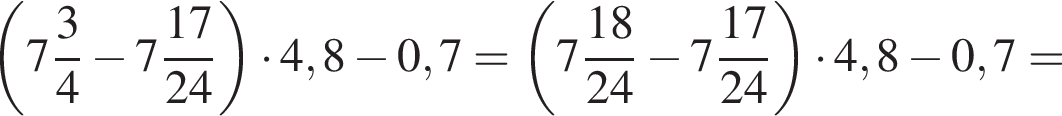
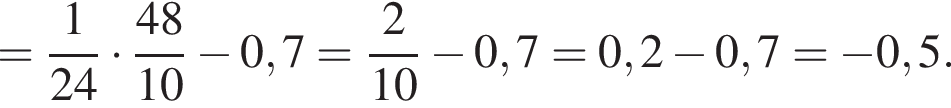
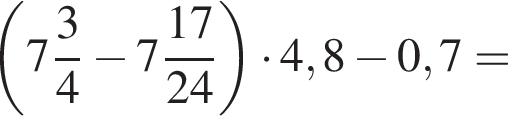
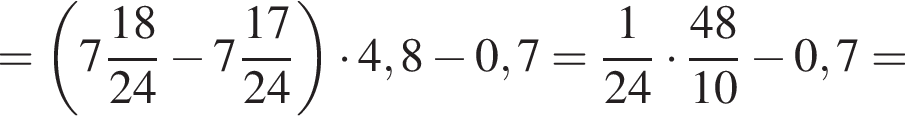
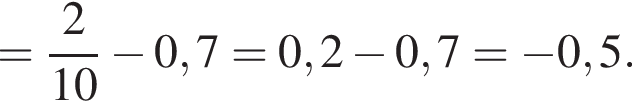
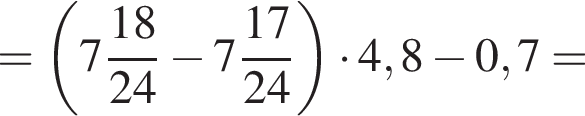
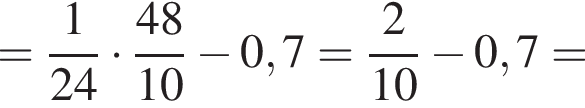
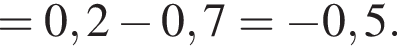
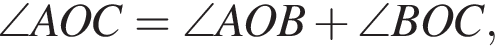
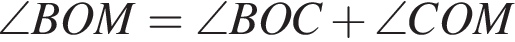 и
и  Таким образом:
Таким образом:
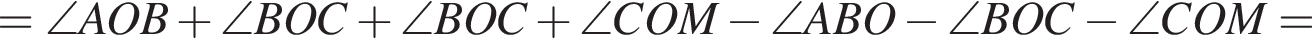
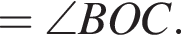

 где r — радиус основания, l — образующая. Найдем радиус:
где r — радиус основания, l — образующая. Найдем радиус: 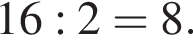 Таким образом, площадь боковой поверхности равна:
Таким образом, площадь боковой поверхности равна: 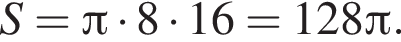
 Тогда:
Тогда: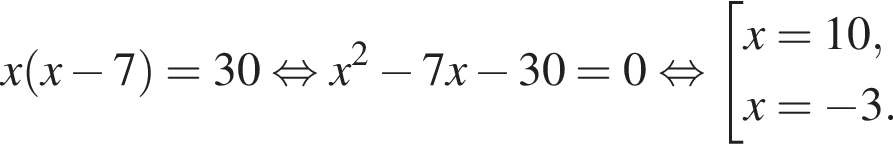
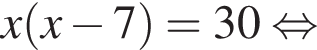
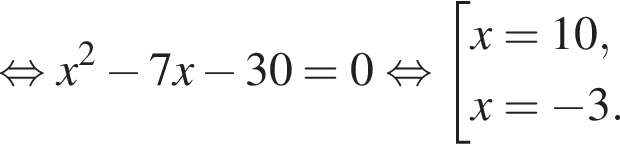
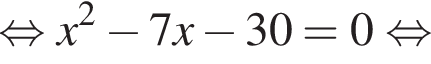
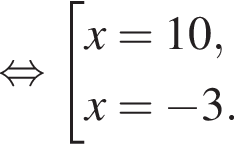
 Тогда получаем:
Тогда получаем: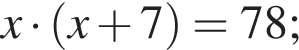
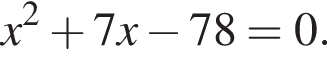

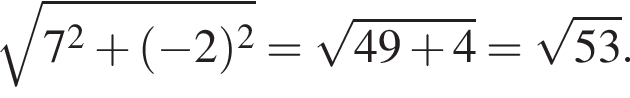 Таким образом, периметр квадрата равен:
Таким образом, периметр квадрата равен: 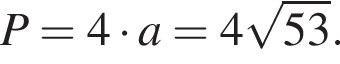

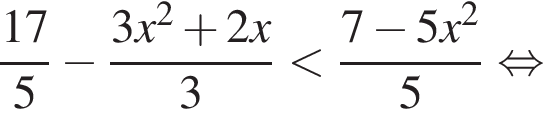
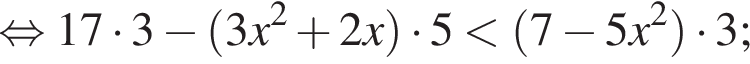
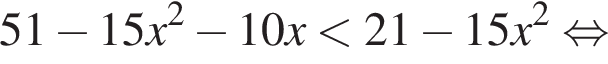

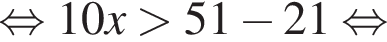

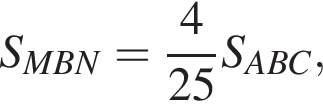 а тогда
а тогда 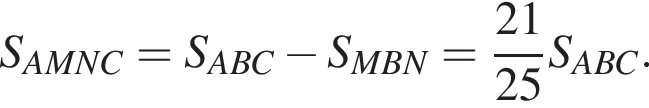
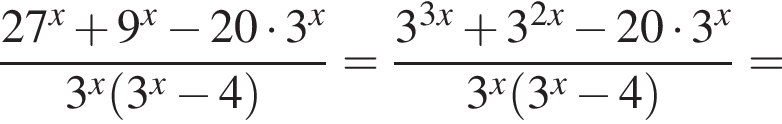
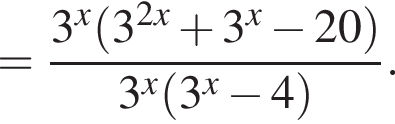
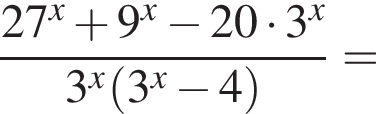
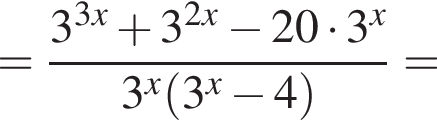
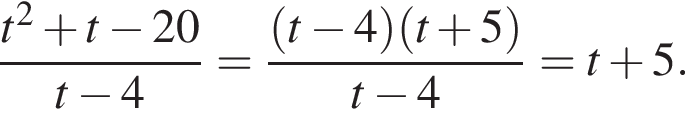 Тем самым, исходное выражение равно
Тем самым, исходное выражение равно 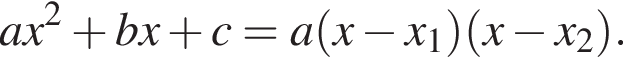
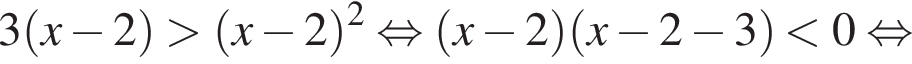

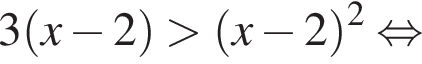
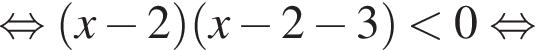
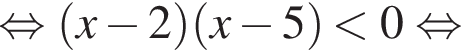

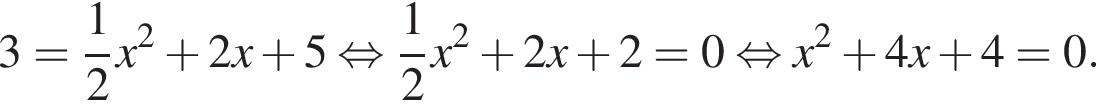
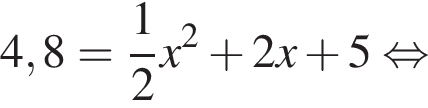
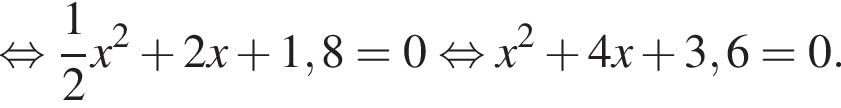
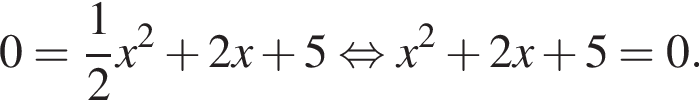 Дискриминант меньше нуля, поэтому пересечений нет.
Дискриминант меньше нуля, поэтому пересечений нет.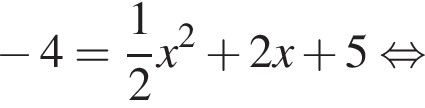
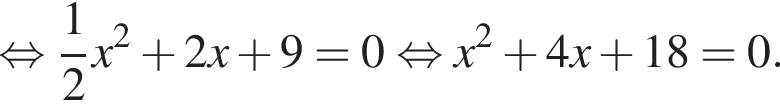
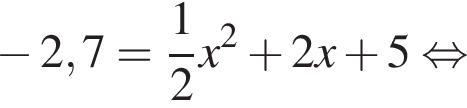
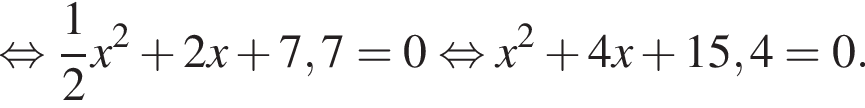
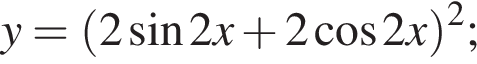
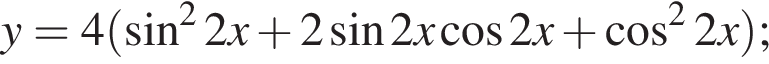

 имеем:
имеем:
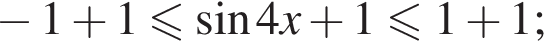
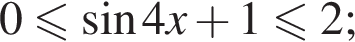
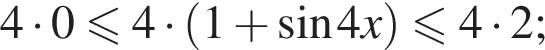
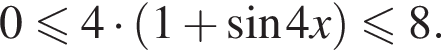
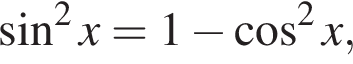 получим:
получим: 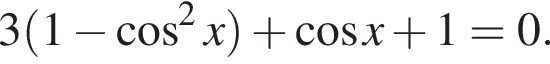 Сделаем замену
Сделаем замену 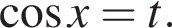 Решим уравнение:
Решим уравнение: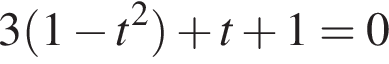
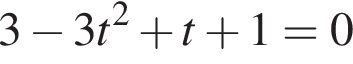
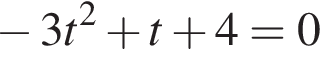
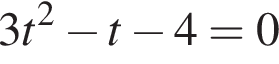
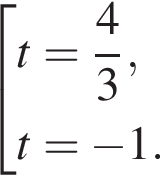
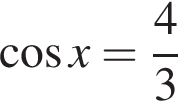 или
или 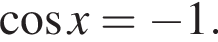 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 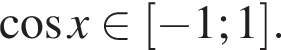 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 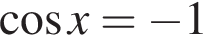

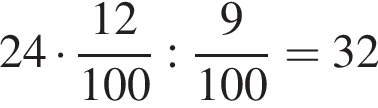 л.
л.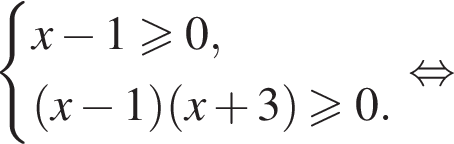
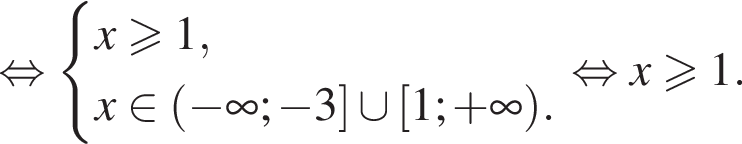
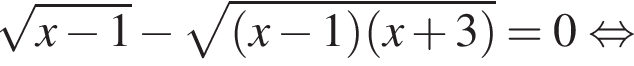
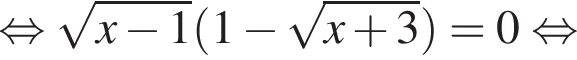
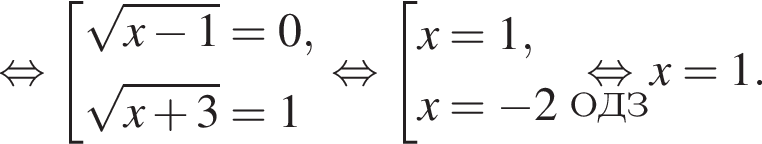
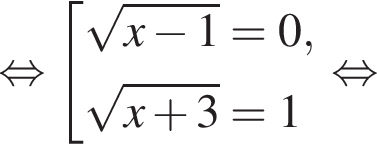
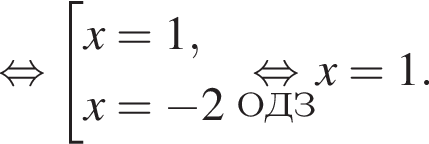
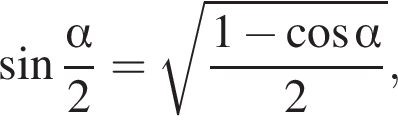 где
где 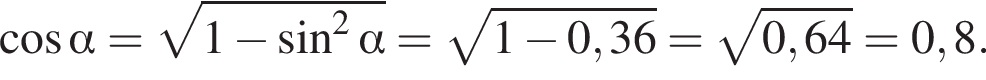
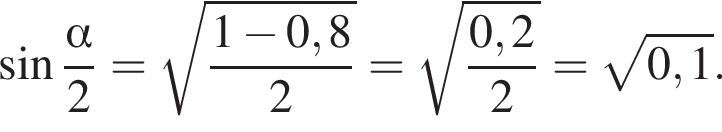
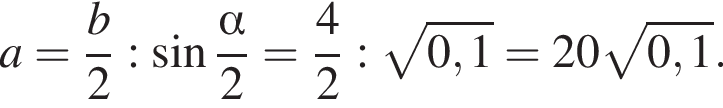
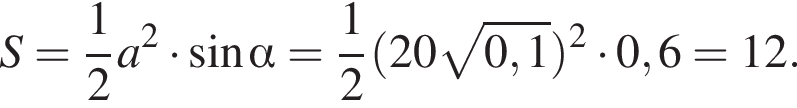
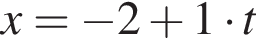 (м) и
(м) и 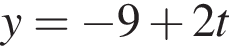 (м).
(м).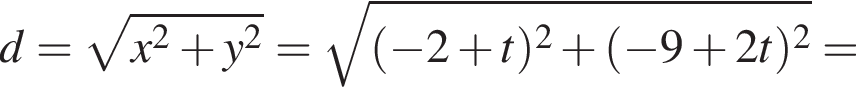
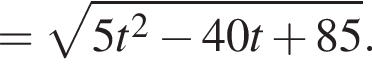
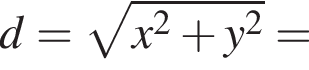
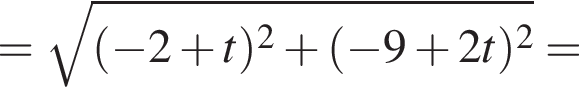
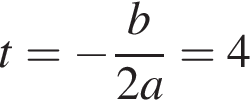 и в этой точке положительно:
и в этой точке положительно: 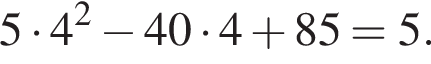 Таким образом, при
Таким образом, при 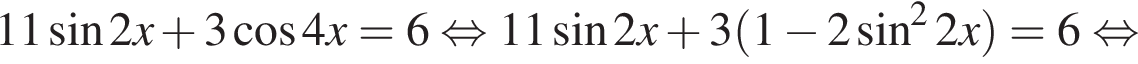
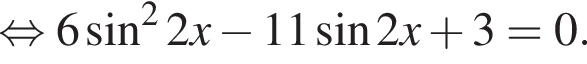
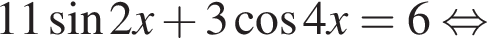
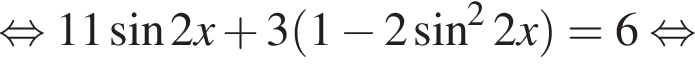
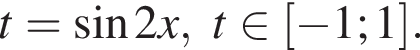 Тогда:
Тогда: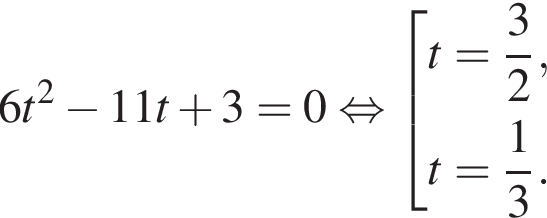
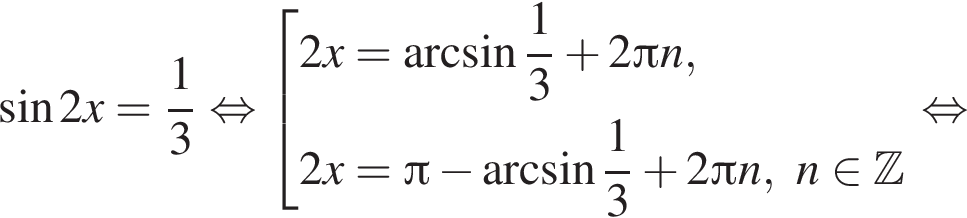
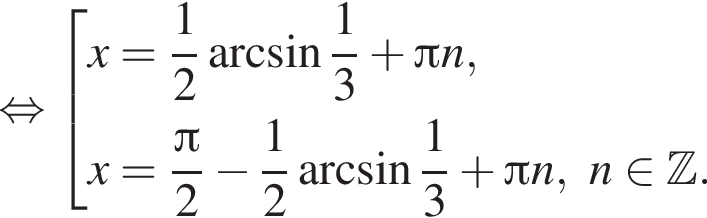
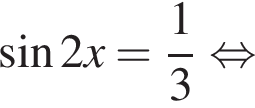
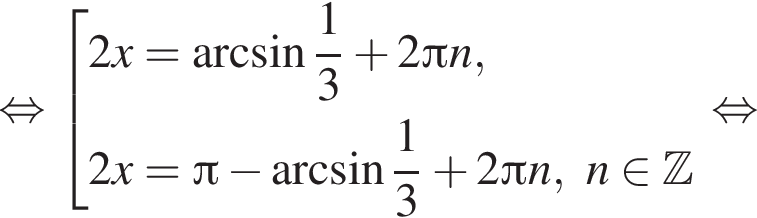
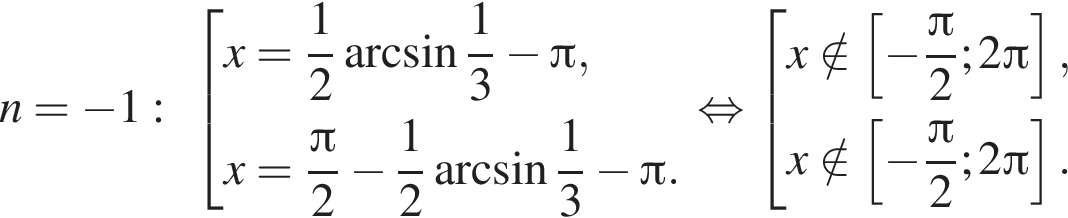
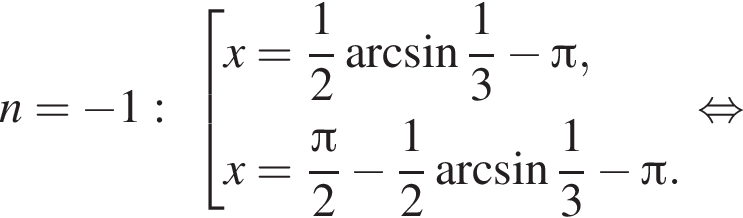
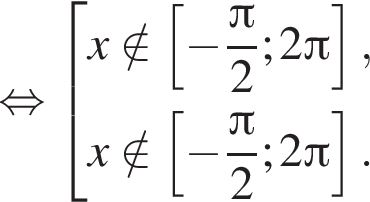
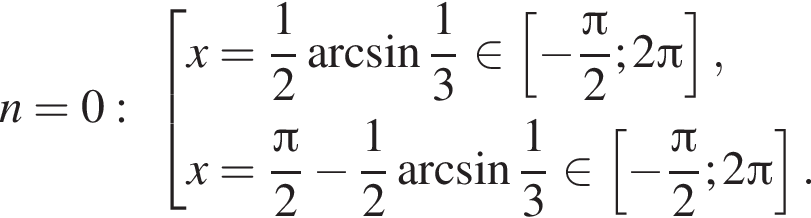
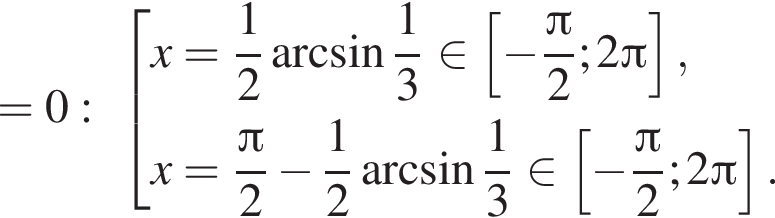
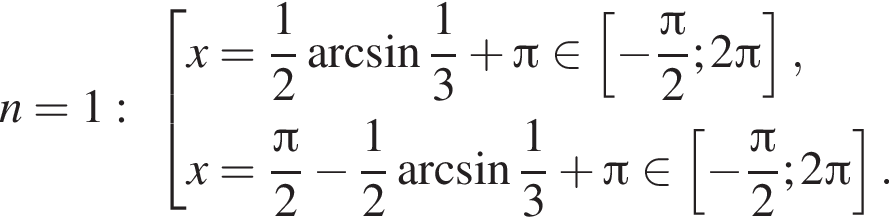
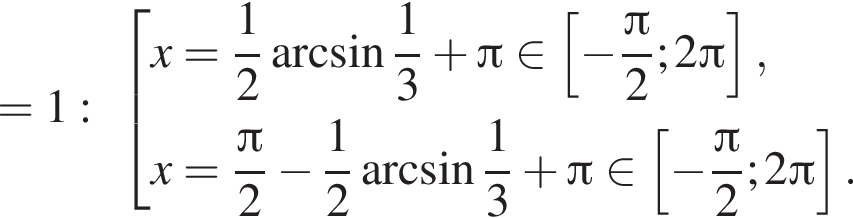
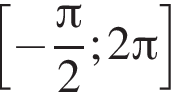 4 корня.
4 корня.




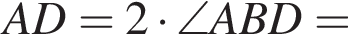
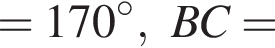
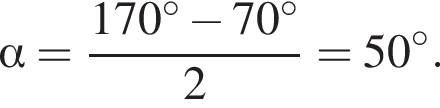
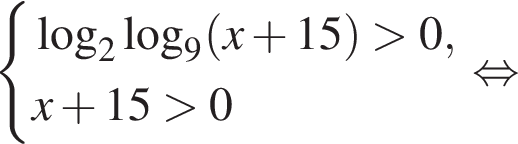
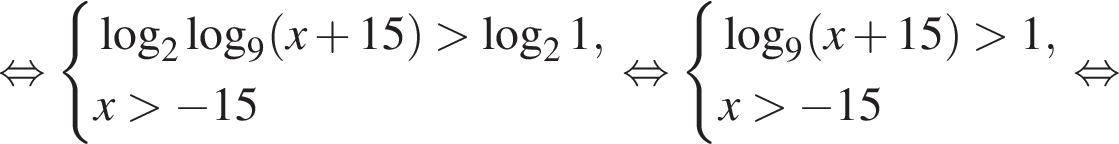
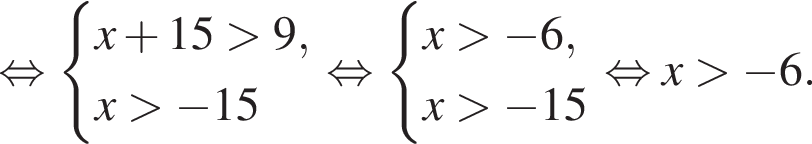
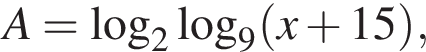 тогда:
тогда: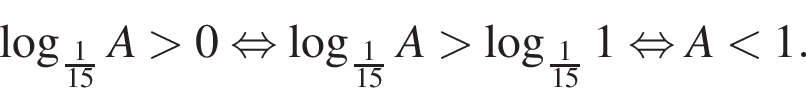
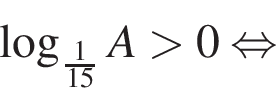
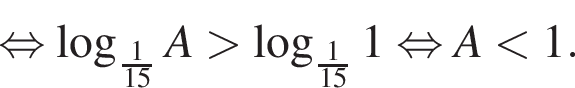

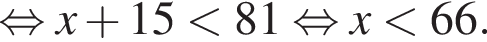


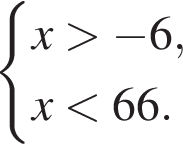 Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.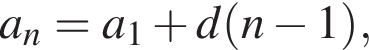 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 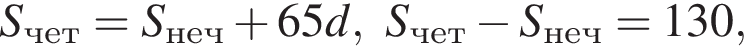 откуда
откуда 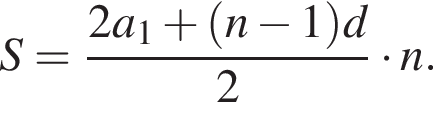 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: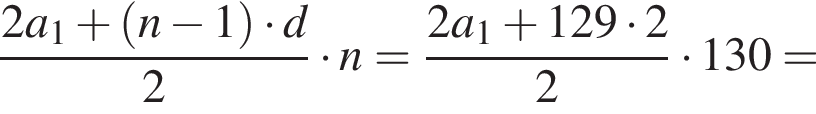
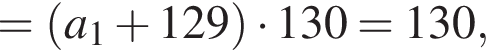
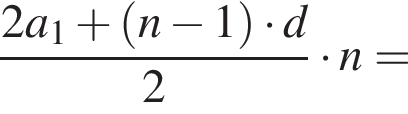
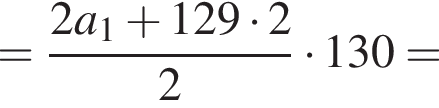
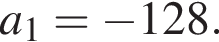 Получим
Получим 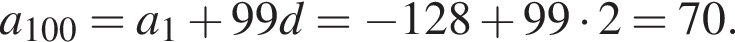
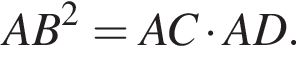 Обозначим AB за x, тогда
Обозначим AB за x, тогда  Тогда:
Тогда: 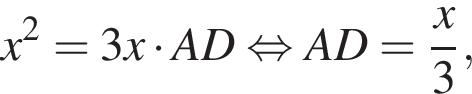 при этом
при этом 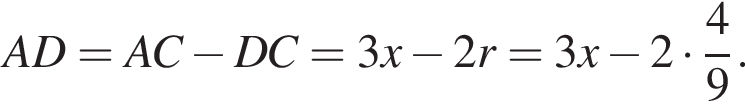 Получим:
Получим: 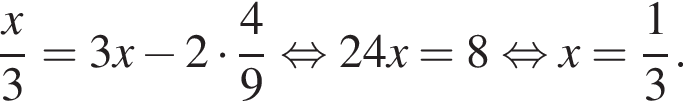
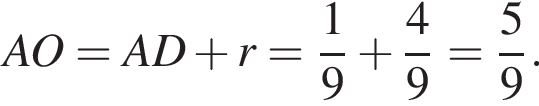
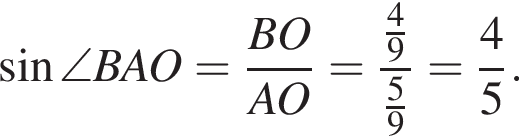 Тогда площадь треугольника ABC:
Тогда площадь треугольника ABC: 
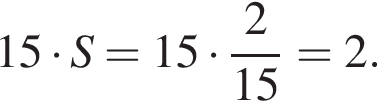
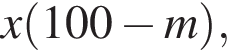 во втором —
во втором — 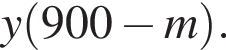 После переливания масса спирта в 1-ом сосуде равна
После переливания масса спирта в 1-ом сосуде равна 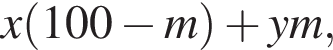 во втором —
во втором —  Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда:
Так как концентрации стали одинаковыми, а объёмы относятся как 1:9, во втором сосуде в 9 раз больше спирта. Тогда: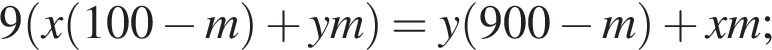
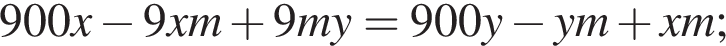

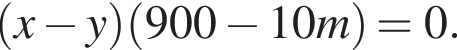

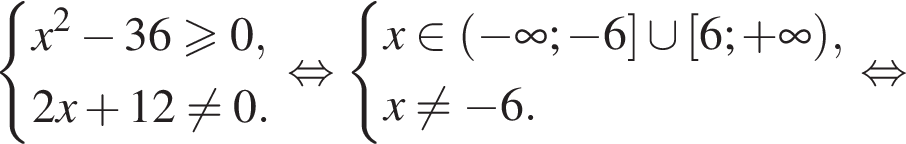

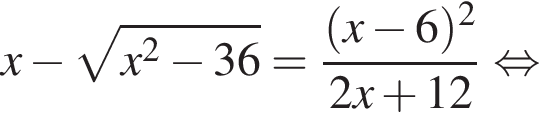
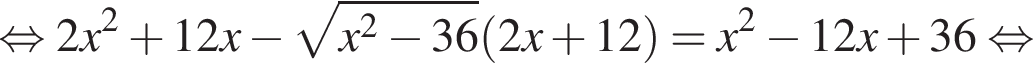
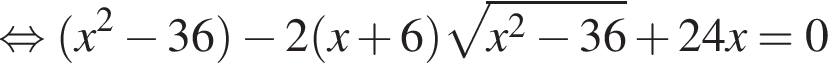
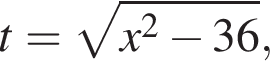 тогда
тогда 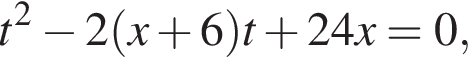 откуда
откуда 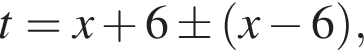 то есть
то есть